Monday, November 12, 2007


Fundamental theorem Limits of functions Continuity Vector calculus Tensor calculus Mean value theorem
Product rule Quotient rule Chain rule Implicit differentiation Taylor's theorem Related rates Table of derivatives
Lists of integrals Improper integrals Integration by: parts, disks, cylindrical shells, substitution, trigonometric substitution
In calculus, a branch of mathematics, the derivative is a measurement of how a function changes when the values of its inputs change. The derivative of a function at a chosen input value describes the best linear approximation of the function near that input value. For a real-valued function of a single real variable, the derivative at a point equals the slope of the tangent line to the graph of the function at that point. In higher dimensions, the derivative of a function at a point is a linear transformation called the linearization.
The process of finding a derivative is called differentiation. The fundamental theorem of calculus states that differentiation is the reverse process to integration.

Differentiation and the derivative
Let y=f(x) be a function of x. In classical geometry, the tangent line at a real number a was the unique line through the point (a, f(a)) which did not meet the graph of f transversally, meaning that the line did not pass straight through the graph. The derivative of y with respect to x at a is, geometrically, the slope of the tangent line to the graph of f at a. The slope of the tangent line is very close to the slope of the line through (a, f(a)) and a nearby point on the graph, for example (a + h, f(a + h)). These lines are called secant lines. A value of h close to zero will give a good approximation to the slope of the tangent line, and smaller values (in absolute value) of h will, in general, give better approximations. The slope of the secant line is the difference between the y values of these points divided by the difference between the x values, that is,
frac{f(a+h)-f(a)}{h}.
This expression is Newton's difference quotient. The derivative is the value of the difference quotient as the secant lines get closer and closer to the tangent line. Formally, the derivative of the function f at a is the limit
f'(a)=lim_{hto 0}{f(a+h)-f(a)over h}
of the difference quotient as h approaches zero, if this limit exists. If the limit exists, then f is differentiable at a. Here f '(a) is one of several common notations for the derivative (see below).
Equivalently, the derivative satisfies the property that
lim_{hto 0}{f(a+h)-f(a) - f'(a)cdot hover h} = 0,
which has the intuitive interpretation (see Figure 1) that the tangent line to f at a gives the best linear approximation
f(a+h) approx f(a) + f'(a)h
to f near a (i.e., for small h). This interpretation is the most easy to generalize to other settings (see below).
Substituting 0 for h in the difference quotient causes division by zero, so the slope of the tangent line cannot be found directly. Instead, define Q(h) to be the difference quotient as a function of h:
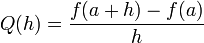Q(h) = frac{f(a + h) - f(a)}{h}.
Q(h) is the slope of the secant line between (a, f(a)) and (a + h, f(a + h)). If f is a continuous function, meaning that its graph is an unbroken curve with no gaps, then Q is a continuous function away from the point h = 0. If the limit 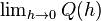textstylelim_{hto 0} Q(h) exists, meaning that there is a way of choosing a value for Q(0) which makes the graph of Q a continuous function, then the function f is differentiable at the point a, and its derivative at a equals Q(0).
In practice, the continuity of the difference quotient Q(h) at h = 0 is shown by modifying the numerator to cancel h in the denominator. This process can be long and tedious for complicated functions, and many short cuts are commonly used to simplify the process.

Definition via difference quotients
The squaring function f(x) = x is differentiable at x = 3, and its derivative there is 6. This is proven by writing the difference quotient as follows:
{f(3+h)-f(3)over h} = {(3+h)^2 - 9over{h}} = {9 + 6h + h^2 - 9over{h}} = {6h + h^2over{h}} = 6 + h.
From the last expression, we see that the difference quotient equals 6 + h when h is not zero and is undefined when h is zero. (Remember that in the definition of the difference quotient, we divided by h, so the difference quotient is always undefined when h is zero.) However, there is a natural way of filling in a value for the difference quotient at zero, namely 6. Hence the slope of the graph of the squaring function at the point (3, 9) is 6, and so its derivative at x = 3 is f '(3) = 6.
More generally, a similar computation shows that the derivative of the squaring function at x = a is f '(a) = 2a.

Example
If y = f(x) is differentiable at a, then f must also be continuous at a. As an example, choose a point a and let f be the step function which returns a value, say 1, for all x less than a, and returns a different value, say 10, for all x greater than or equal to a. f cannot have a derivative at a. If h is negative, then a + h is on the low part of the step, so the secant line from a to a + h will be very steep, and as h tends to zero the slope tends to infinity. If h is positive, then a + h is on the high part of the step, so the secant line from a to a + h will have slope zero. Consequently the secant lines do not approach any single slope, so the limit of the difference quotient does not exist. Informally, this means that differentiable functions are very atypical among continuous functions. The first known example of a function that is continuous everywhere but differentiable nowhere is the Weierstrass function.

Derivative Continuity and differentiability
Let f be a function that has a derivative at every point a in the domain of f. Because every point a has a derivative, there is a function which sends the point a to the derivative of f at a. This function is written f'(x) and is called the derivative function or the derivative of f. The derivative of f collects all the derivatives of f at all the points in the domain of f.
Sometimes f has a derivative at most, but not all, points of its domain. The function whose value at a equals f'(a) whenever f'(a) is defined and is undefined elsewhere is also called the derivative of f. It is still a function, but its domain is strictly smaller than the domain of f.
Using this idea, differentiation becomes a function of functions: The derivative is an operator whose domain is the set of all functions which have derivatives at every point of their domain and whose range is a set of functions. If we denote this operator by D, then D(f) is the function f′(x). Since D(f) is a function, it can be evaluated at a point a. By the definition of the derivative function, D(f)(a) = f′(a).
For comparison, consider the doubling function f(x) =2x; f is a real-valued function of a real number, meaning that it takes numbers as inputs and has numbers as outputs:
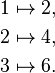
begin{align}<br /> 1 &{}mapsto 2,<br /> 2 &{}mapsto 4,<br /> 3 &{}mapsto 6.<br /> end{align}
The operator D, however, is not defined on individual numbers. It is only defined on functions:
begin{align}<br /> (x mapsto 1) &{}mapsto (x mapsto 0),<br /> (x mapsto x) &{}mapsto (x mapsto 1),<br /> (x mapsto x^2) &{}mapsto (x mapsto 2x).<br /> end{align}
Because the output of D is a function, the output of D can be evaluated at a point. For instance, when D is applied to the squaring function,
x mapsto x^2,
D outputs the doubling function,
x mapsto 2x ,
which we named f(x). This output function can then be evaluated to get f(1) = 2, f(2) = 4, and so on.

The derivative as a function
Let f be a differentiable function, and let f'(x) be its derivative. The derivative of f'(x) (if it has one) is written f''(x) and is called the second derivative of f. Similarly, the derivative of a second derivative, if it exists, is written f'''(x) and is called the third derivative of f. These repeated derivatives are called higher-order derivatives.
A function f need not have a derivative, for example, if it is not continuous. Similarly, even if f does have a derivative, it may not have a second derivative. For example, let
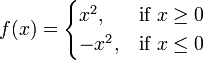f(x) = begin{cases} x^2, & mbox{if }xge 0 -x^2, & mbox{if }x le 0end{cases}.
An elementary calculation shows that f is a differentiable function whose derivative is
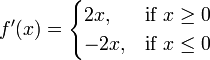f'(x) = begin{cases} 2x, & mbox{if }xge 0 -2x, & mbox{if }x le 0end{cases}.
f'(x) is twice the absolute value function, and it does not have a derivative at zero. Similar examples show that a function can have k derivatives for any non-negative integer k but no (k + 1)-order derivative. A function that has k successive derivatives is called k times differentiable. If in addition the kth derivative is continuous, then the function is said to be of differentiability class C. (This is a stronger condition than having k derivatives. For an example, see differentiability class.) A function that has infinitely many derivatives is called infinitely differentiable or smooth.
On the real line, every polynomial function is infinitely differentiable. By standard differentiation rules, if a polynomial of degree n is differentiated n times, then it becomes a constant function. All of its subsequent derivatives are identically zero. In particular, they exist, so polynomials are smooth functions.
The derivatives of a function f at a point x provide polynomial approximations to that function near x. For example, if f is twice differentiable, then
f(x+h) approx f(x) + f'(x)h + tfrac12 f''(x) h^2
in the sense that
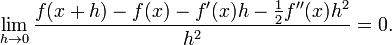
lim_{hto 0}frac{f(x+h) - f(x) - f'(x)h - frac12 f''(x) h^2}{h^2}=0.
If f is infinitely differentiable, then this is the beginning of the Taylor series for f.

Higher derivatives

Main article: Notation for differentiation Notations for differentiation

Main article: Leibniz's notation Leibniz's notation
One of the most common modern notations for differentiation is due to Joseph Louis Lagrange and uses the prime mark, so that the derivative of a function f(x), is denoted f'(x), or simply f',. Similarly, the second and third derivatives are denoted (f')'=f'', and ((f')')'=f''',. Beyond this point, some authors use Roman numerals such as f^{IV}, for the fourth derivative, whereas other authors place the number of derivatives in parentheses: f^{(4)}, in this case. The latter notation generalizes to yield the notation f^{(n)}, for the nth derivative of f.

Lagrange's notation

Main article: Newton's notation Newton's notation
Euler's notation uses a differential operator D, which is applied to a function f to give the first derivative Df. The second derivative is denoted Df.
If y=f(x) is a dependent variable, then often the subscript x is attached to the D to clarify the independent variable x. Euler's notation is then written Dxy or Dxf(x), although this subscript is often omitted when the variable x is understood, for instance when this is the only variable present in the expression.
Euler's notation is useful for stating and solving linear differential equations.

Euler's notation
The derivative of a function can, in principle, be computed from the definition by considering the difference quotient, and computing its limit. For some examples, see Derivative (examples). In practice, once the derivatives of a few simple functions are known, the derivatives of other functions are more easily computed using rules for obtaining derivatives of more complicated functions from simpler ones.

Computing the derivative

Main article: Differentiation rules Rules for finding the derivative

Main article: Table of derivatives Derivatives of elementary functions
The derivative of
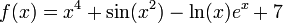
f(x) = x^4 + sin (x^2) - ln(x) e^x + 7,
is
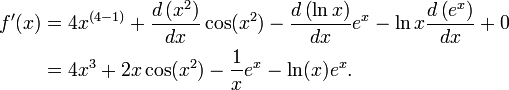
<br /> begin{align}<br /> f'(x) &= 4 x^{(4-1)}+ frac{dleft(x^2right)}{dx}cos (x^2) - frac{dleft(ln {x}right)}{dx} e^x - ln{x} frac{dleft(e^xright)}{dx} + 0 <br /> &= 4x^3 + 2xcos (x^2) - frac{1}{x} e^x - ln(x) e^x.<br /> end{align}<br />
Here the second term was computed using the chain rule and third using the product rule: the known derivatives of the elementary functions x were also used.

Example computation
See also: vector calculus and multivariable calculus

Derivatives in higher dimensions
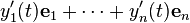A vector-valued function y(t) of a real variable is a function which sends real numbers to vectors in some vector space R, then y(t) can also be written as y_1(t)mathbf{e}_1 + cdots + y_n(t)mathbf{e}_n . If we assume that the derivative of a vector-valued function retains the linearity property, then the derivative of y(t) must be y'_1(t)mathbf{e}_1 + cdots + y'_n(t)mathbf{e}_n, because each of the basis vectors is a constant.
This generalization is useful, for example, if y(t) is the position vector of a particle at time t; then the derivative y'(t) is the velocity vector of the particle at time t.

Derivatives of vector valued functions

Main article: Partial derivative Partial derivatives

Main article: Directional derivative Directional derivatives

Main article: Total derivative The total derivative, the Jacobian, and the differential

Main article: Derivative (generalizations) Generalizations

Online books

Automatic differentiation
Differentiability class
Differintegral
Linearization
Numerical differentiation
Techniques for differentiation
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)