Einstein · Hawking . Friedman · Lemaître · Hubble · Penzias · Wilson · Gamow · Dicke · Zel'dovich · Mather · Smoot · others
The Friedmann-Lemaître-Robertson-Walker (FLRW) metric is an exact solution of the Einstein field equations of general relativity; it describes a homogeneous, isotropic expanding or contracting universe. Depending on geographical or historical preferences, a subset of the four scientists -- Alexander Friedmann, Georges Lemaître, Howard Percy Robertson and Arthur Geoffrey Walker -- may be named (e.g., Friedmann-Robertson-Walker (FRW) or Robertson-Walker (RW) or Friedmann-Lemaître (FL)).

General Metric
The metric leaves some choice of normalization. One common choice is to say that scale factor is 1 today (). In this choice the coordinate r carries dimensionality as does k. In this choice k does not equal ±1 or 0 but .
Another choice is to specify that k is ± 1 or 0. This choice makes 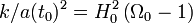where the scale factor now carries the dimensionality and the coordinate r is dimensionless.
The metric is often written in a curvature normalized way via the transformation
In curvature normalized coordinates the metric becomes
where for k greater than, equal to, and less than 0 respectively. This normalization assumes the scale factor is dimensionless but it can be easily converted to normalized k.
The comoving distance is distance to an object with zero peculiar velocity. In the curvature normalized coordinates it is χ. The proper distance is the physical distance to a point in space at an instant in time. The proper distance is .

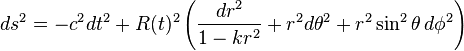Normalization
This metric has an analytic solution to the Einstein field equations G_μν − Λg_μν = 8πT_μν giving the Friedmann equations when the energy-momentum tensor is similarly assumed to be isotropic and homogeneous. The resulting equations are:
These equations serve as a first approximation of the standard big bang cosmological model including the current ΛCDM model. Because the FLRW assumes homogeneity, some popular accounts mistakenly assert that the big bang model cannot account for the observed lumpiness of the universe. In a strictly FLRW model, there are no clusters of galaxies, stars or people, since these are objects much denser than a typical part of the universe. Nonetheless, the FLRW is used as a first approximation for the evolution of the universe because it is simple to calculate, and models which calculate the lumpiness in the universe are added onto FLRW as extensions. Most cosmologists agree that the observable universe is well approximated by an almost FLRW model, that is, a model which follows the FLRW metric apart from primordial density fluctuations. As of 2003, the theoretical implications of the various extensions to FLRW appear to be well understood, and the goal is to make these consistent with observations from COBE and WMAP.

Solutions
The above pair of equations is equivalent to the following pair of equations
with k serving as a constant of integration for the second equation.
The first equation can be derived also from thermodynamical considerations and is equivalent to the first law of thermodynamics, assuming the universe expansion is an adiabatic process (which is implicitly assumed in the derivation of the Friedmann-Lemaître-Robertson-Walker metric).
The second equation states that both the energy density and the pressure causes the universe expansion rate to decrease, i.e. both cause a decceleration in the expansion of the universe. This is a consequence of gravity, with pressure playing a similar role to that of energy (or mass) density, according to the principles of general relativity. The cosmological constant, on the other hand, causes an acceleration in the expansion of the universe.

Interpretation
The cosmological constant term can be omitted if we make the following replacement
Therefore the cosmological constant can be interpreted as arising from a form of energy which has negative pressure, equal in magnitude to its (positive) energy density:
p = − u.
Such form of energy - a generalization of the notion of a cosmological constant - is known as dark energy.
In fact, in order to get a term which causes an acceleration of the universe expansion, it is enough to have a scalar field which satisfies
p < − u / 3.
Such a field is sometimes called quintessence.

Name and History
Einstein's radius of the universe is radius of curvature of space of Einstein's universe, a long-abandoned static model that was supposed to represent our universe in idealized form. Putting 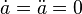in the Freidman equation, the radius of curvature of space of this universe (Einstein's radius) is 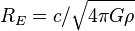, where c is the speed of light, G is the Newtonian gravitational constant, and ρ is the density of space of this universe. The numerical value of Einstein's radius is of order of 10 light years.